Prueba de unidad. ¡Sube de nivel en todas las habilidades en esta unidad y obtén hasta 1500 Puntos de Dominio! En Álgebra 2 se introdujeron los números complejos a los estudiantes, y realizaron operaciones básicas con ellos. En esta unidad ampliamos este concepto y realizamos operaciones más sofisticadas, como la división de números.. Los números complejos son los puntos en el plano, expresados como pares ordenados (a, b), donde a representa la coordenada para el eje horizontal y b representa la coordenada para el eje vertical. Consideremos el número − 2 + 3i. La parte real del número complejo es − 2 y la parte imaginaria es 3.
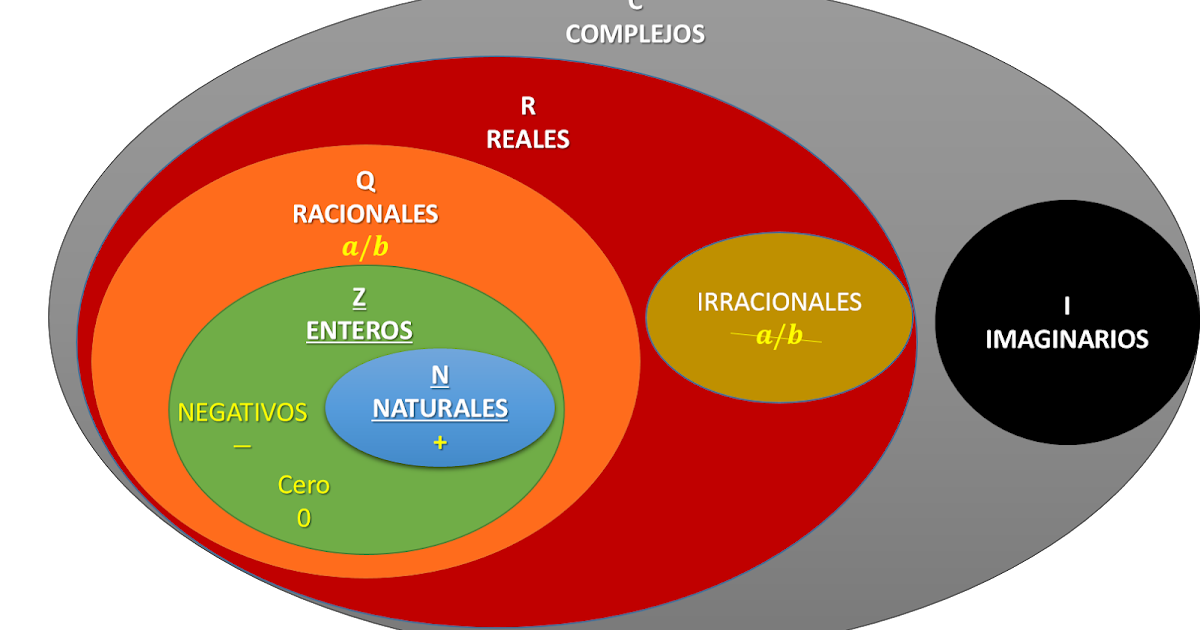
Matemáticas Fáciles Clasificación de los Números Complejos

Números complejos Propiedades YouTube

Los Números Complejos Math4all

CÓMO se Suman NÚMEROS COMPLEJOS Operaciones con los NÚMEROS COMPLEJOS Ejercicios resueltos YouTube

PPT Los números complejos. PowerPoint Presentation, free download ID4846686
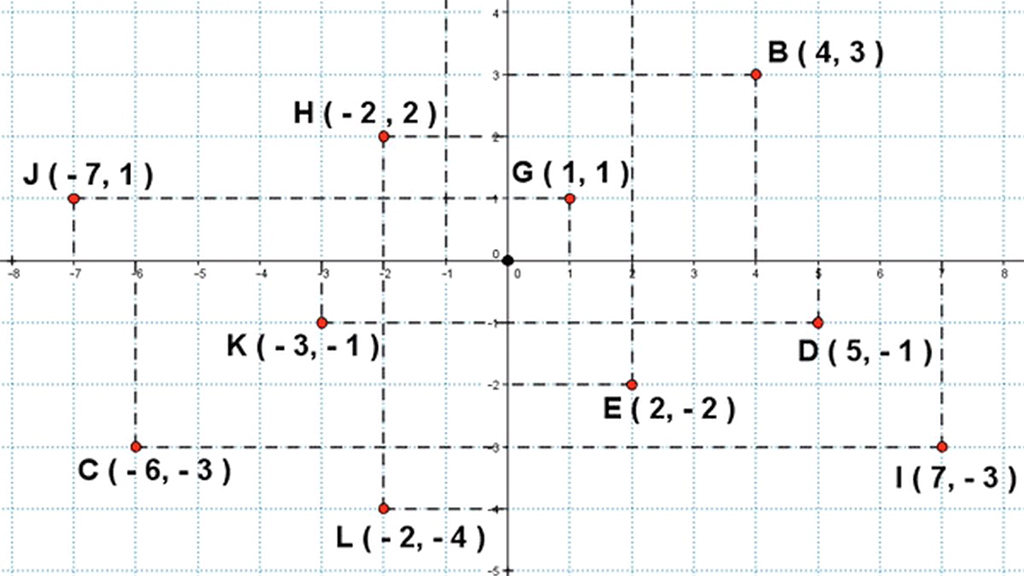
Los Números Complejos Math4all

Números complejos Esquemat

Números complejos Esquemat

Números COMPLEJOS RESUMEN con ejemplos y ejercicios (con soluciones!!)

Propiedades del conjugado y de la magnitud de los complejos YouTube

OPERACIONES CON NÚMEROS COMPLEJOS YouTube

Propiedades Del Argumento De Un Numero Complejo SeanhasBuck

Álgebra Propiedades de los números complejos. Partial differential equation, Differential

04. Propiedades de la multiplicación de números complejos YouTube

Propiedades, Fórmulas Números Complejos

NUMEROS COMPLEJOS EJERCICIOS RESUELTOS PDF

Propiedades de Numeros Complejos Número complejo Multiplicación

Cálculo21 Demostración de una propiedad del módulo de números complejos

Numeros complejos
.gif)
NUMEROS COMPLEJOS EJERCICIOS RESUELTOS PDF
Origen de los Números Complejos. Los números complejos se originan al resolver ecuaciones como x² + 1 = 0, cuyas soluciones son \( \sqrt{-1} \) ,esta ecuación no admite soluciones en el campo de los números reales. Entonces se define el campo de los números complejos que englobe estas soluciones y a los números reales que conocemos.. LOS NÚMEROS COMPLEJOS. El sistema de números complejos, construido a partir de los números reales, tienen propiedades heredadas de éstos como las propiedades sobre la suma y la multiplicación. Recuerde que dos números complejos, z1 = a1 +b1i z 1 = a 1 + b 1 i y z2 = a2 +b2i z 2 = a 2 + b 2 i son iguales si y sólo si son iguales sus.