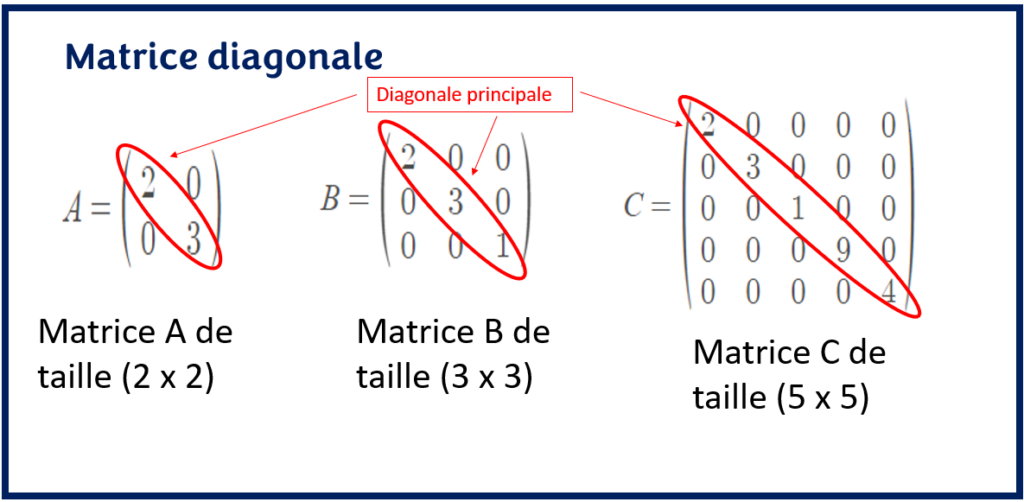
son polynôme caractéristique étant . En mathématiques, une matrice diagonalisable est une matrice carrée semblable à une matrice diagonale. Cette propriété est équivalente à l’existence d’une base de vecteurs propres, ce qui permet de définir de manière analogue un endomorphisme diagonalisable d’un espace vectoriel .. Qu’est ce qu’une matrice diagonale ? (Définition) Une matrice diagonale est une matrice dont les éléments hors de la trace (la diagonale principale) sont tous nuls. La diagonalisation est une transformation utilisée en algèbre linéaire afin de pouvoir ensuite réaliser des calculs plus facilement. Qu’est ce qu’une matrice diagonalisable ?

Diagonalisation d’une matrice exercice YouTube
MATRICES LANGAGE MATRICIEL

Vérifier si une matrice est diagonalisable YouTube

Diagonalisation simultanée “naïve” de 2 matrices carrées YouTube

Notion de matrice DIAGONALISABLE et de base de vecteurs propres pr une matrice diagonalisable

Matrice Diagonalisable avec valeurs propres multiples YouTube

Diagonalisation of matrix, example II YouTube
Inverse d’une matrice diagonale

vérifier si une matrice est diagonalisable YouTube
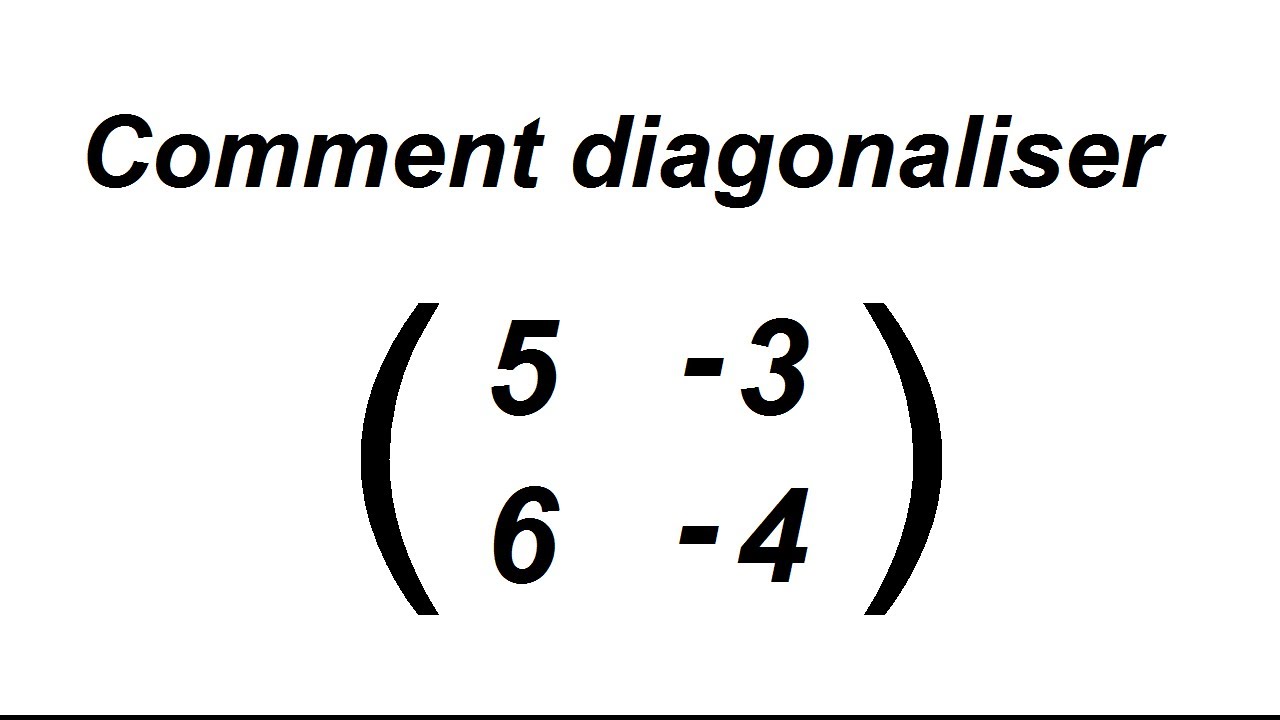
Comment diagonaliser une matrice 2×2 partie 1 YouTube

EXERCICE PROBABILITÉS CALCULER LA PROBABILITÉ QU’UNE MATRICE SOIT DIAGONALISABLE YouTube

Montrer qu’une matrice est inverse d’une autre matrice Terminale maths expertes YouTube

Montrer qu’une matrice n’ est pas inversible par absurde YouTube

Diagonalisation. Exercice corrigé diagonalisation d’une matrice. ( Partie 3 ) YouTube
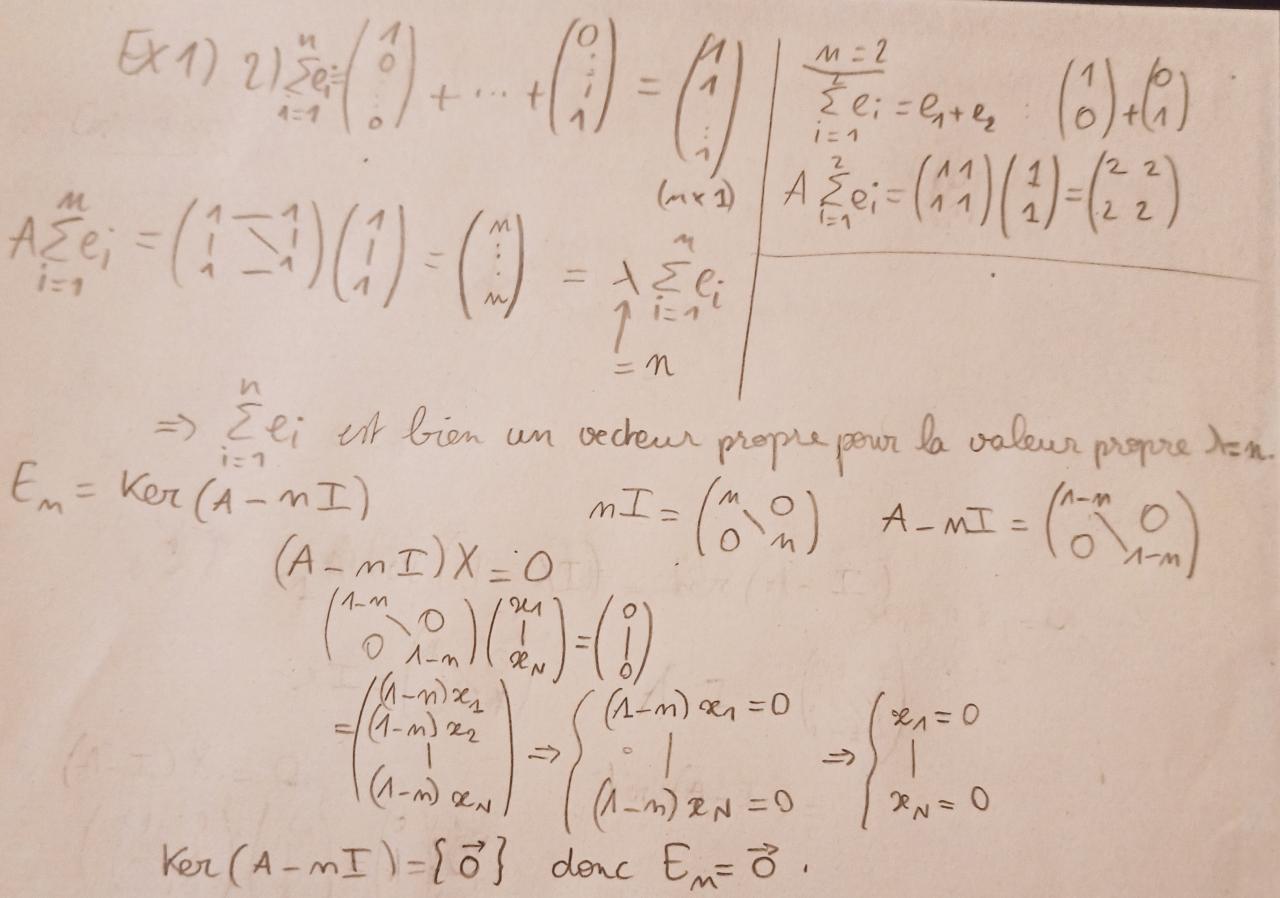
Exercice matrice diagonalisable
Puissance d’une matrice diagonale

Matrice diagonalisable Définition YouTube

Résoudre EDP avec une matrice diagonalisable YouTube

DIAGONALISER DES MATRICES 3×3 SYMETRIQUES. EXERCICE CONCOURS. Algèbre. Maths Spé. YouTube
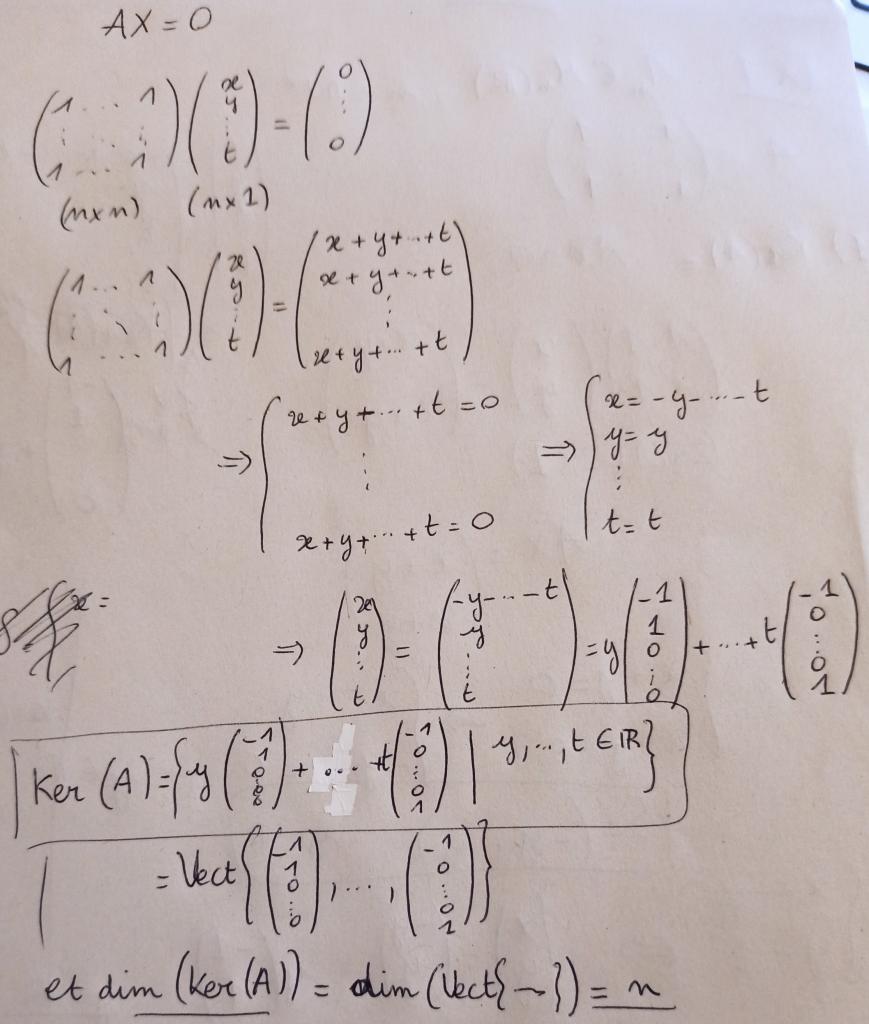
Exercice matrice diagonalisable
Universit e Paul Verlaine { Metz Ann ee universitaire 2010-2011 Pr eparation concours 2 (L2, BE) A. Pasquale Par la suite M n(R) d enote l’espace vectoriel des matrices carr ees n na coe cients r eels, muni des op erations habilituelles d’addition et de multiplication par un nombre r eel.. Caractérisation de la diagonalisabilité avec les vecteurs propres ou avec les espaces propres , matrices admettant un maximum de valeurs propres. Compétences. Déterminer si une matrice est diagonalisable à l’aide de la recherche de ses valeurs propres et vecteurs propres. Diagonaliser une matrice ou un endomorphisme.