Comment calcule l’aire d’un triangle ? Formule expliquée en détail. Exemples de calculs.Retrouvez cette vidéo et d’autres sur le même thème sur la page https.. L’aire d’un triangle est, en géométrie euclidienne, une mesure de la surface plane déterminée par trois points et les segments joignant ces points. L’intérêt de l’aire d’un triangle provient du fait que tout polygone peut être scindé en triangles. Il existe plusieurs méthodes de calcul de cette aire, suivant ce qui est connu du triangle, la plus connue étant celle utilisant une.
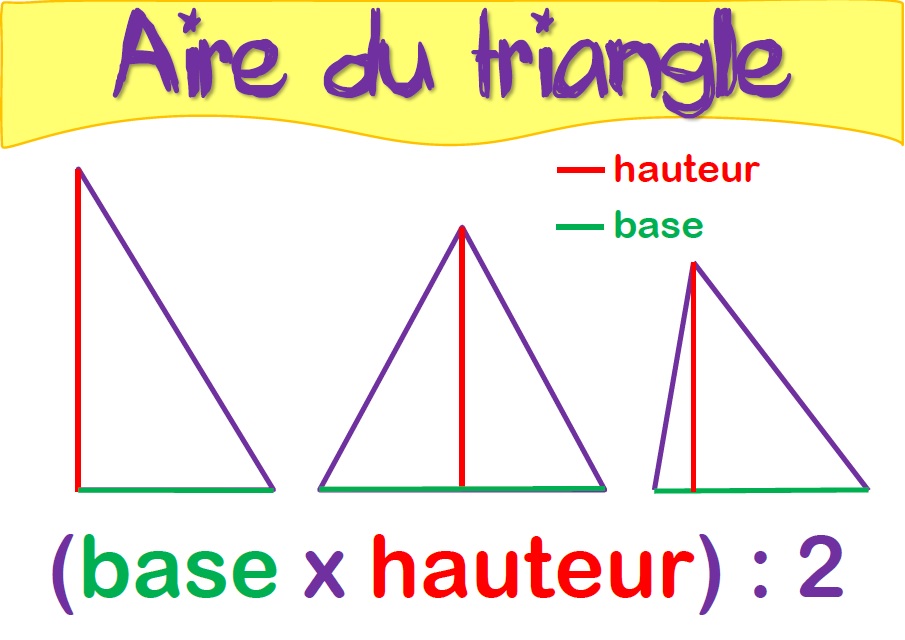
Une affiche pour l’aire du triangle MA MAITRESSE DE CM1CM2

Aire d’un triangle Corrigés d’exercices AlloSchool

Comment calculer l’aire du triangle

Calculer l’aire de chaque triangle. Nosdevoirs.fr

Comment Calculer L Aire D Un Triangle Isocele AUTOMASITES

Comment calculer l’aire d’un triangle rectangle (formule) YouTube

Comment calculer l’aire d un triangle sans connaitre la hauteur YouTube
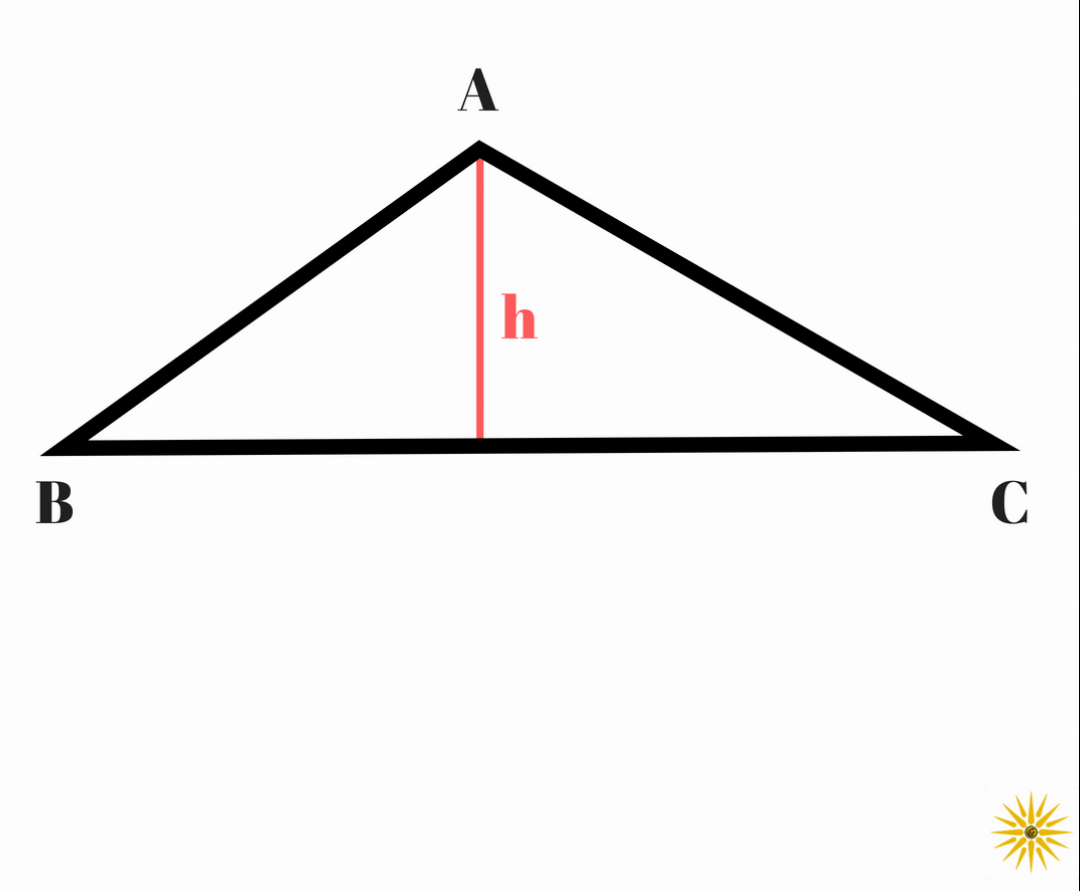
Calculer l’aire d’un triangle méthode

Comment calculer l’aire d’un triangle YouTube

Démonstration Formule de l’aire d’un triangle YouTube
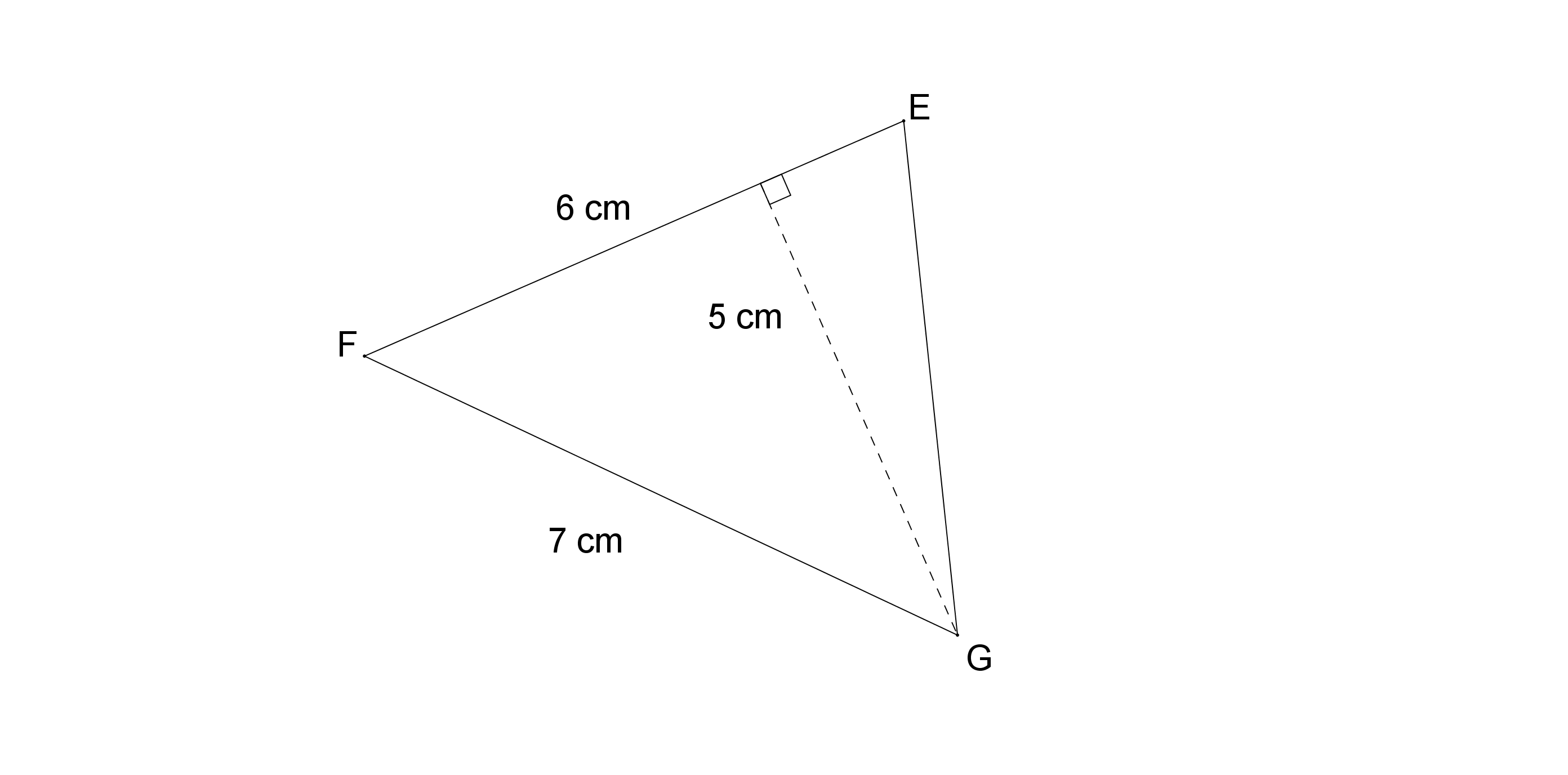
Exercice 2 aire d’un triangle Mathplace

Les formes géométriques Comment calculer le Périmètre et l’aire d’un triangle YouTube
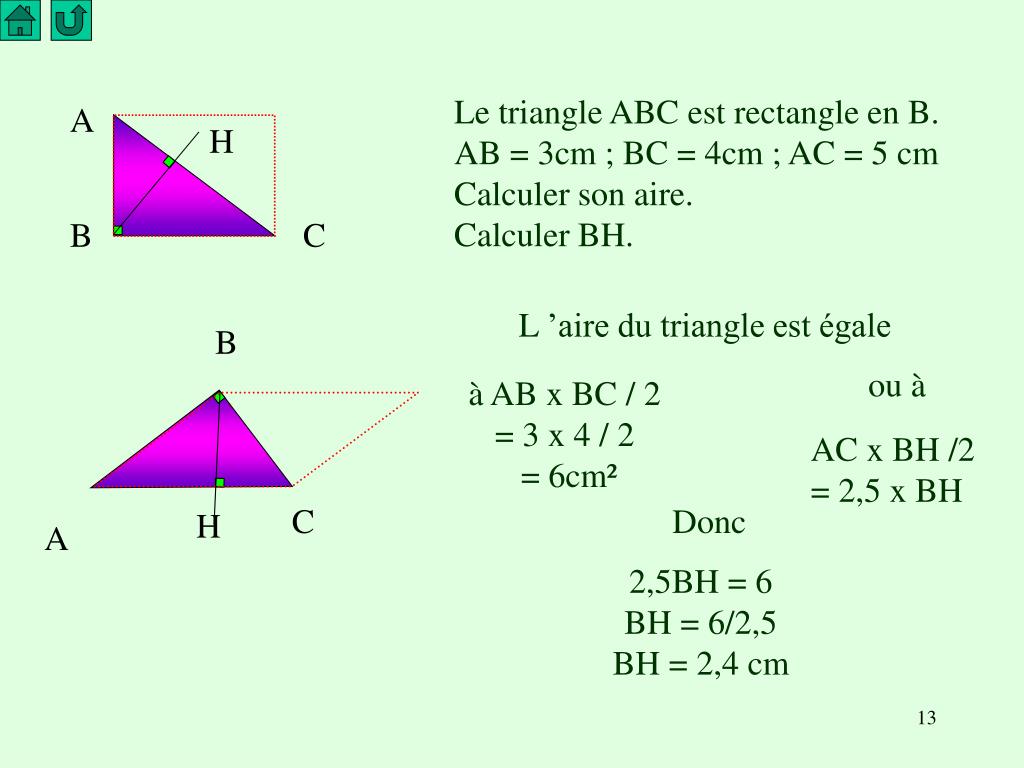
PPT L ’aire du triangle. PowerPoint Presentation, free download ID4582181

Comment calculer l aire d un triangle rectangle isocèle formule YouTube

Quelle est l’aire d’un triangle? Exercice de mathématiques secondaire YouTube

Aire d’un triangle Cours de maths YouTube
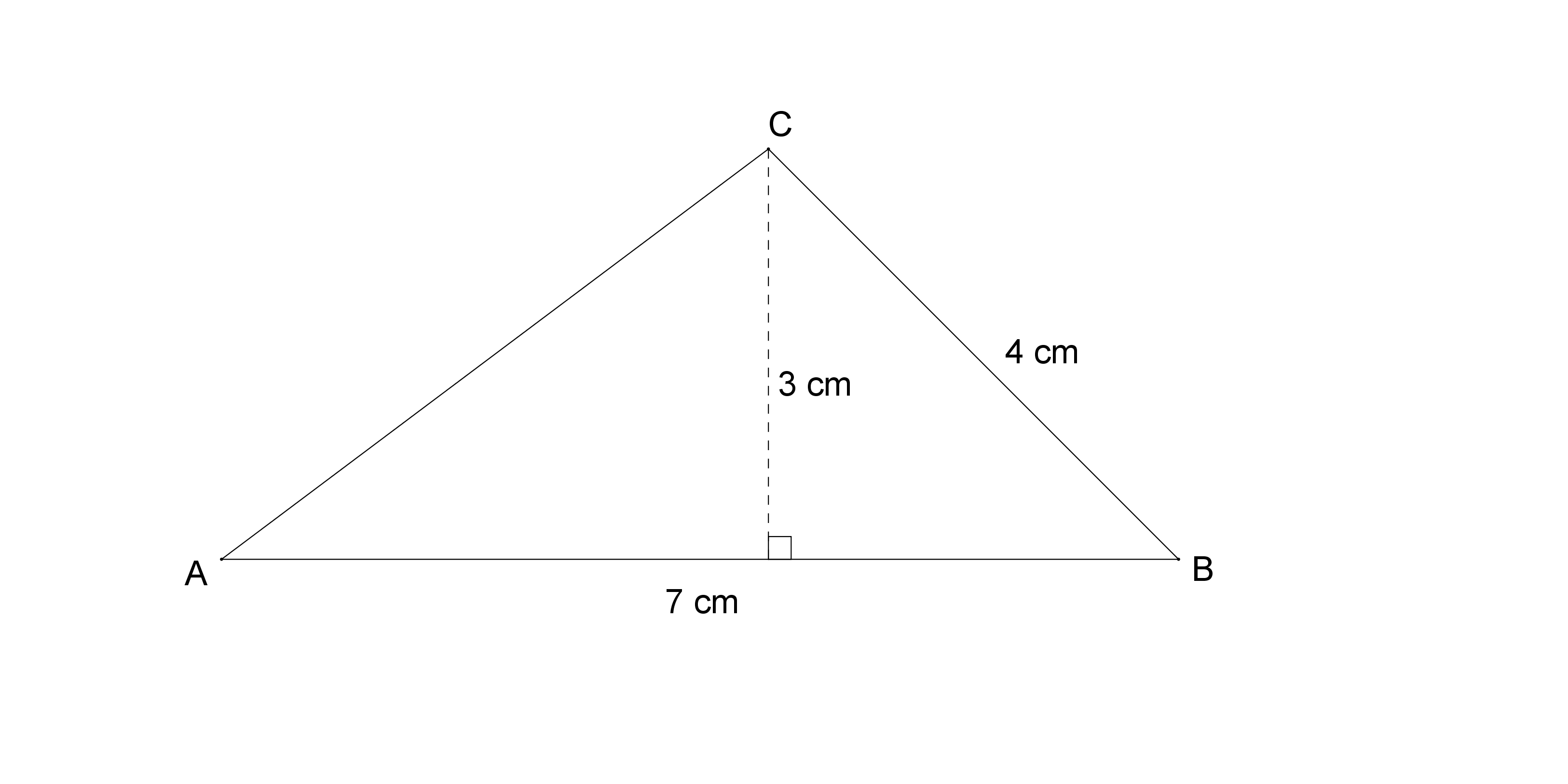
Exercice 1 aire d’un triangle Mathplace
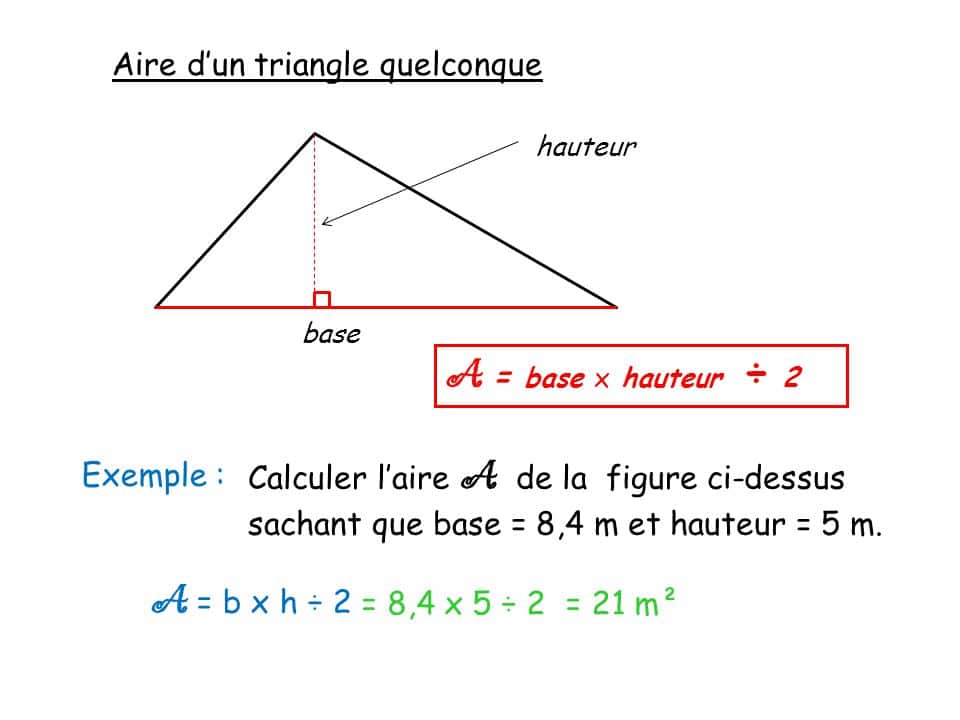
Calcul aire triangle Maelynn.fr

Calculer l’Aire d’un Polygone

Lernen Ecke aus calculer l aire d un triangle rectangle Strich Ernst einfach
Découvrez facilement l’aire d’un triangle avec notre calculateur d’aire triangulaire gratuit ! Vous pouvez calculer avec la base et la hauteur, trois côtés différents et bien d’autres. Fonctionne avec des angles et des radians ! Aire d’un triangle par sa hauteur et sa base. Hauteur. Base. Zone.. Pour calculer l’aire d’un triangle, la longueur d’un côté avec la hauteur correspondante est suffisante. En utilisant ces deux valeurs données, l’aire du triangle peut être déterminée. Nous traiterons de ce cas dans la section suivante sous “Aire d’un triangle de côté connu et de hauteur correspondante h”.