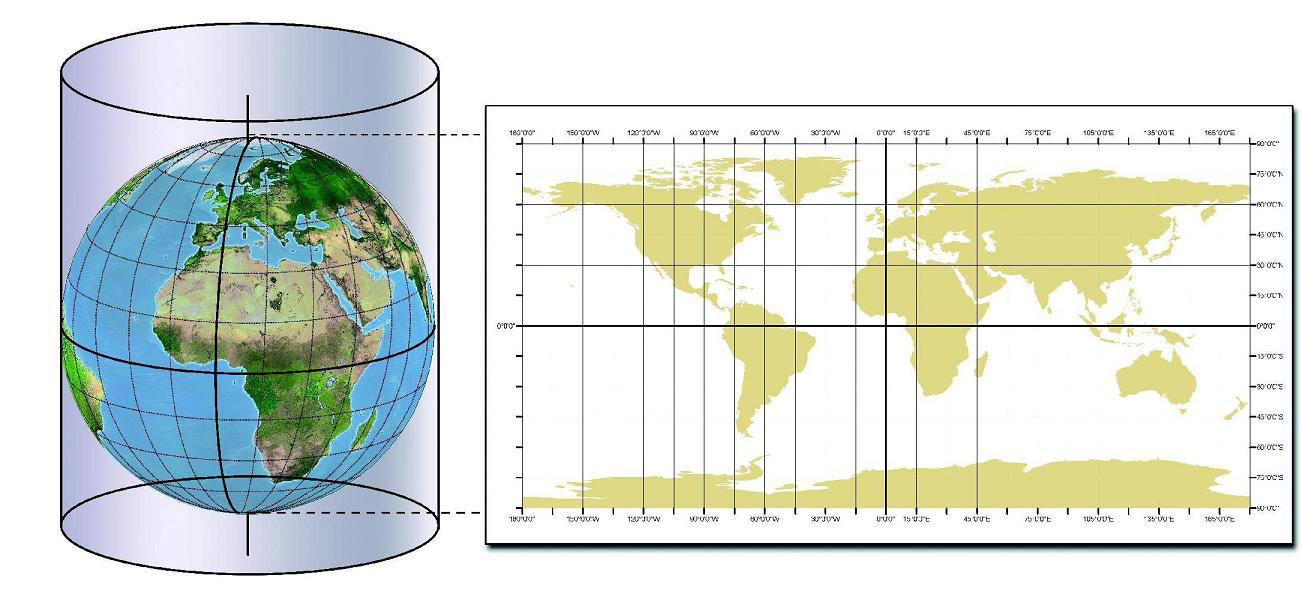
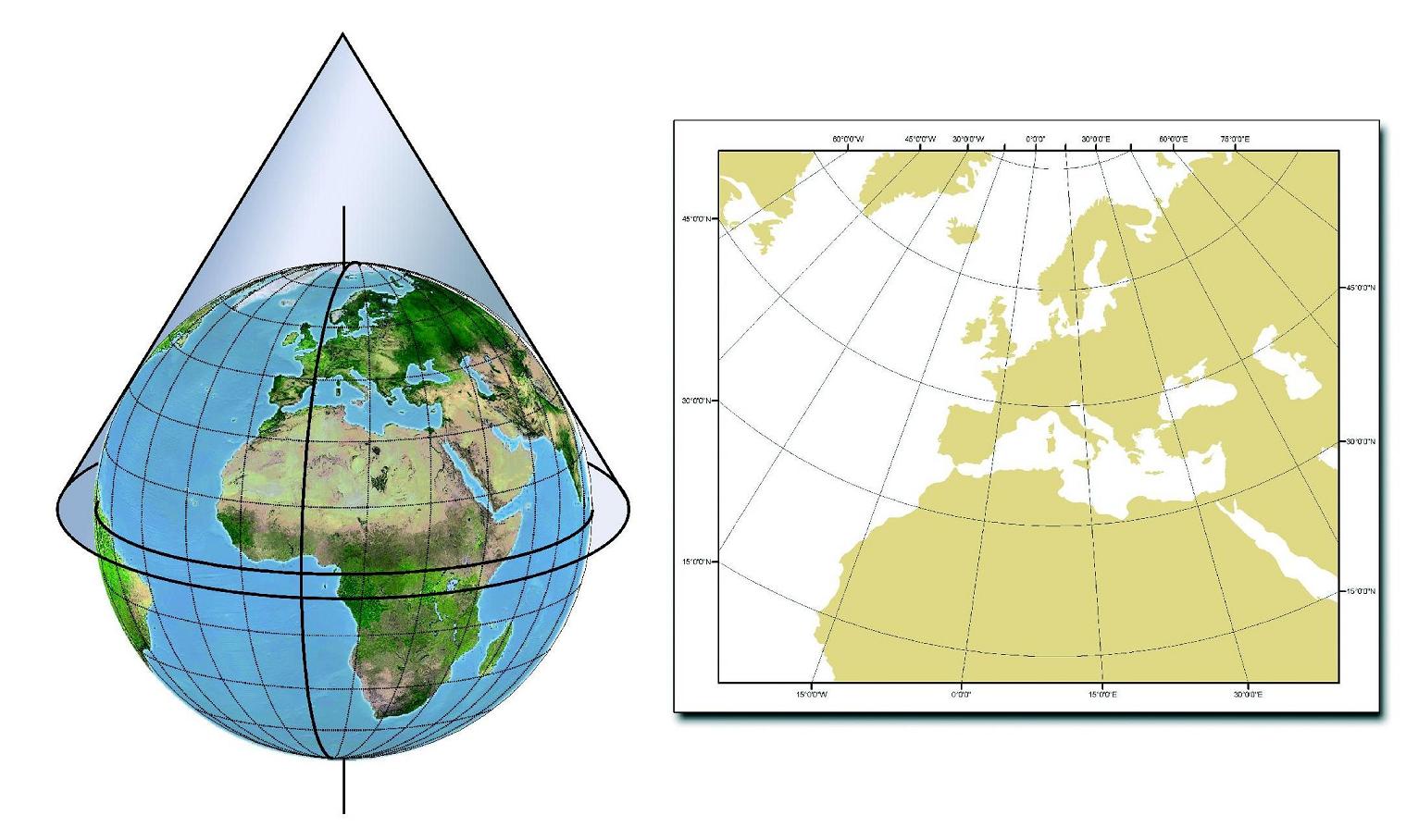
La proyección cónica cartográfica se caracteriza por proyectar los puntos de una superficie esférica sobre la superficie de un cono, cuyo vértice se ubica sobre el eje que pasa por los polos y es tangente o secante a la esfera. El cono es una superficie que se puede abrir en un plano, formando un sector angular y sin deformar las líneas proyectadas sobre él.. Ejemplos de proyecciones cartográficas. La proyección de Winkel-Tripel se considera el mejor modelo de representación terrestre. Las principales y más conocidas proyecciones cartográficas de la Tierra (o sea, un mapamundi) son: La proyección de Mercator. Creada por el geógrafo y matemático alemán Gerardus Mercator (1512-1594) en 1569.

PROYECCIÓN CÓNICA Conforme de Lambert para Bolivia (CCLB) ArcGis 10.2 YouTube

Proyección cónica

El Margen de Fermat Tema 6Lugares Geométricos. Cónicas.1ºBach.CT
Proyección cónica cartográfica características, ventajas, desventajas

Proyecciones cónicas Proyecciones cónicas La proyección cónica más simple es aquella en que el

☑ Proyecciones cartográficas

Diseño de Información PROYECCIÓN CÓNICA SIMPLE
Entendiendo las proyecciones en SIG Gis&Beers

Husos horarios y Representación de la Tierra

Diseño de Información PROYECCIÓN CÓNICA SIMPLE

Perspectiva cónica Dibujos paso a paso Web del maestro

PROYECCION CONICA

Sistemas de proyección Instituto Geográfico Nacional
Entendiendo las proyecciones en SIG Gis&Beers

Proyecciones de la tierra
el blog de plástica perspectiva cónica. Introducción

Dibujos perspectiva cónica Web del maestro

Diseño de Información PROYECCIÓN CÓNICA SIMPLE
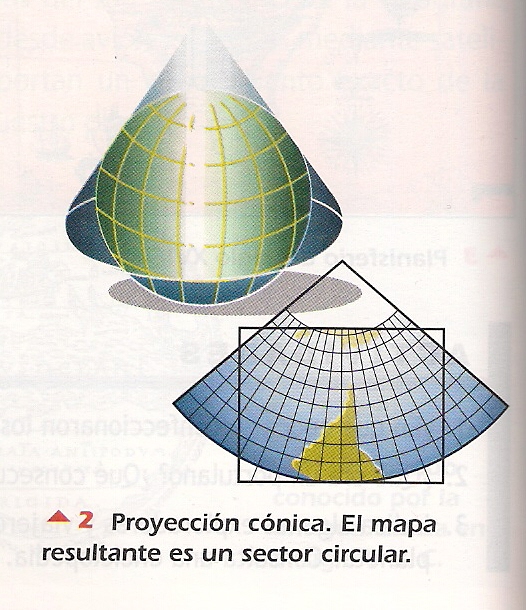
De Esperanza a dos minutos Sistemas de proyección.
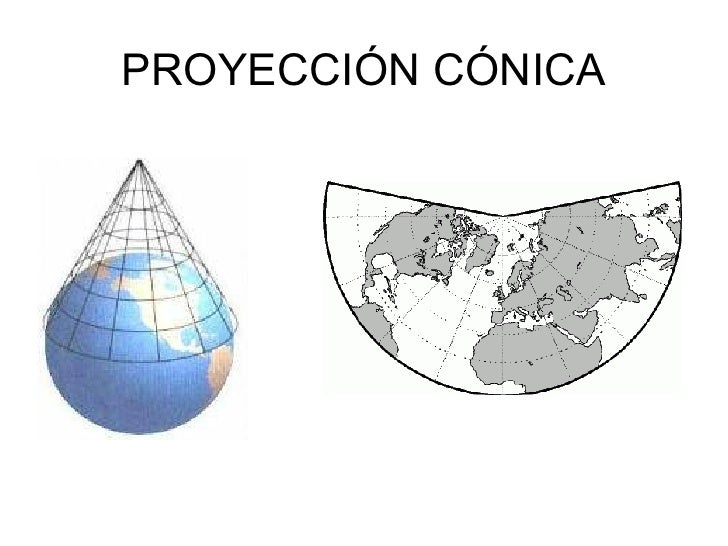
Geografia 1
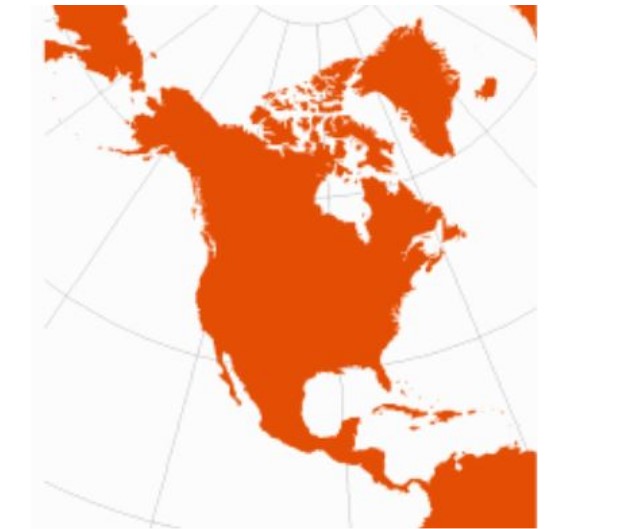
Mapamundi con la proyección de Mercator de 1569. Las propiedades de la proyección cartográfica. Si bien resulta imposible no deformar la Tierra cuando se proyecta sobre un plano, gracias a las matemáticas podemos aplicar una modificación que nos permita mantener alguno de los parámetros importantes que interesan conocer a la hora de leer un mapa: distancia, superficie y forma (o.. Retícula. La proyección cónica conforme de Lambert es una proyección cónica. Todos los meridianos son líneas rectas equidistantes que convergen en un punto común: el polo más cercano a los paralelos estándar. Los paralelos se representan como arcos circulares centrados en el polo. Su espaciado aumenta al alejarse de los paralelos.